这几天一直谣传所谓的“复杂性理论”(complexity theory)领域出现了数年一见的大进展,可能会给互联网领域带来新的曙光。
这么说没错——因为新的突破与网络之间的比较有关,正可以应用于人与人之间的互联网联结。芝加哥大学的数学家与计算机科学家拉斯洛•鲍鲍伊(László Babai)发现了一种数学方法,可以用比之前少得多的步骤来判断两个网络是不是完全相同的,不管这些网络有多复杂或缠结。计算机科学界已经炸开了锅,因为很多难以解决的问题最终都可以归结到比较两个网络是否相同这一任务上。
“如果这一方法是对的,它可能会成为计算机理论领域十年来最重要的成果。”麻省理工学院的计算机科学家、博客作者斯科特•阿伦森(Scott Aaronson)说。
所谓复杂性理论,从根本上说就是研究哪些工作可以很容易地用计算机完成,哪些工作不能的理论。在复杂性理论中,最关键的事情是搞清楚随着输入数据的增长,解决一个问题所需的步骤会以什么样的方式增加。举个例子:如果你想知道一个给定的数,比如983或105227是不是素数(即只能被1和它自己整除的数),那计算机所要进行的步骤随着给定数字位数的增长就相对比较缓慢,大体上以类似n的几次方的速度增长(n为位数)。像n^2这样的表达式被称为多项式(polynomial),因此该问题就被称为可以在“多项式时间”内解决,复杂度类别为P。
而另一方面,如果你想要把一个数,如21112331分解质因数,即分解成质数相乘的形式,到现在为止还没有人找到一个可以在多项式时间内解决该问题的算法。因此,分解质因数被认为是一个更难的问题,被归类到更宽范围内的“NP”问题之列,即“不确定性多项式”(nondeterministic polynomial)问题。简单来说,对于NP问题,随着输入数据位数的增加,所需步骤会呈指数式增长,如2^n,它增长得比n^2快得多(举个例子,100^2只等于10000,而2^100则超过了10的24次方)。
而现在,鲍鲍伊找出了一个新算法,将一个原本被认为属于NP的问题变得更接近较为容易的P问题。问题是这样的:无论是传染流感的人群,还是与生物体发生相互作用的蛋白质,都可以抽象为一系列的点(计算机专业术语称为“节点”,node),它们之间的相互关系则用连接点的直线(称为“边”,edge)来表示。由于节点可以被任意地拖来拖去,所以即使是两个看起来完全不同的图,其连接方式也可能是完全相同的(见下图)。所谓的“图同构问题”(graph isomorphism problem),其主要任务就是确定两个图究竟是相同的,还是不同的,而鲍鲍伊宣称已经找到一种新的算法来解决这个问题。
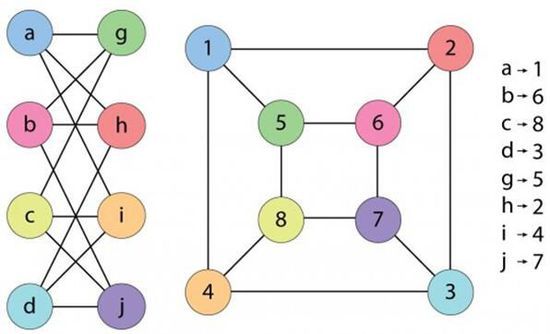
图同构问题中的任务,就是判定两个看起来明显不同的图能否经过重组变得完全相同——就像图中的两个图一样。图片来源:WIKIPEDIA COMMONS
此前,这个问题最好的解决方法是俄勒冈大学的数学家与计算机科学家尤金•卢克斯(Eugene Luks)在1983年提出的,他的方法所需要的步骤几乎随节点数目按指数增长,而鲍鲍伊的算法所需要的步骤只比多项式增长稍多一些。虽然在外行人看来“指数增长”和“多项式增长”差别不大,但对于计算机专家来说这个定性的区别却是极为激动人心的。“假如结果真的成立,这就是计算机理论科学领域一颗闪耀的明珠。”在麻省理工学院计算机科学家阿伦森的博客中,有读者这样评论道。其他的博客里也有读者表示:“超级让人激动!”
不过,出乎意料的是,尽管我们生活中到处都有网络和图,鲍鲍伊的新算法的应用范围却不会很大。阿伦森说,现有的算法已经可以非常快速地解决大多数图的同构问题了,如果鲍鲍伊的新方法成立,也只是证明少数极为复杂的图也能用高效的方法处理。复杂性理论中最大的问题,是“NP”型问题是否真正不同于“P”型问题——研究者通常认为回答是肯定的,否则类似互联网加密之类的技术就会变得极其易受攻击,但到此为止还没人能严格证明NP≠P,鲍鲍伊的成果连这个问题的边都没挨到呢。
那么鲍鲍伊的新算法的意义在何处呢?阿伦森说,它真正的成就,是把一个关键问题从难题转变成为了简单问题。图同构问题曾经一直被认为是一个非常古怪的问题:它是一个难题,但其本身一些特性又与一些简单问题相关;而到了现在,鲍鲍伊直接把它变成了一个简单问题。
当然,他的工作还得经过其他研究者的检验。他于11月11日在芝加哥大学做了一次报告展示他的算法,在24日还将再做一次。阿伦森说:“我们还得看看他的算法中的细节。要知道,即使是鲍鲍伊这样的科学家,也是可能犯错的。”(撰文:阿德里安•丘(Adrian Cho) 翻译:丁家琦)

