在复杂系统/网络中,我们总是希望系统中各个节点的状态能够变化到想要的状态,这个任务或者说问题就是复杂网络系统控制性问题[1].
这个描述看起来很抽象,但是他跟公司、社会和系统的有序性、方向性和调控性有很大的关系。也能帮助我们理解下面的问题:为什么有些公司规模不大但是内斗严重、上传下达沟通困难,为什么领导忽略底层员工的声音常常会导致对公司/组织现状的重大误判,为什么社交网络上人们的意见容易被操控,为什么公司内各个部门之间的目标不一致导致大量的无用功或者功用抵消,为什么基因编辑牵一发而动全身而往往导致意料之外的后果,为什么关于大脑的认知功能的某方面缺陷或者锻炼总是能引发全局的认知功能和性能的变化,为什么按照现有架构设计的脑机接口系统没有什么发展前途,为什么计算集群系统的容灾设计必须演化成现在这个样子,为什么推荐系统的引入必然导致整个社区的退化和分化,为什么西方社会的政府相比于中国政府控制疫情的能力薄弱,为什么股票/期货市场难以被大范围操控等等。
在具体讨论之前,我们先引入一些简化该问题的数学定义。
经典的线性时不变系统动态方程可以写成以下形式:
其中向量 是系统中
个节点的状态向量。
是
矩阵,
描述系统中 个节点之间的相互关系,
是
输入矩阵,且
.
是控制者可调控的时变输入向量。通常地,
能引发系统中多个节点状态的变化。所以我们实际上没有必要控制系统中全部的节点,而是只需要控制其中的子集。一般来说,存在一个最小节点子集,包括
个节点,能让我们能控制整个系统到任何状态。易证明,当控制矩阵
满秩时候,也就是
时,系统是可控的[2][3].
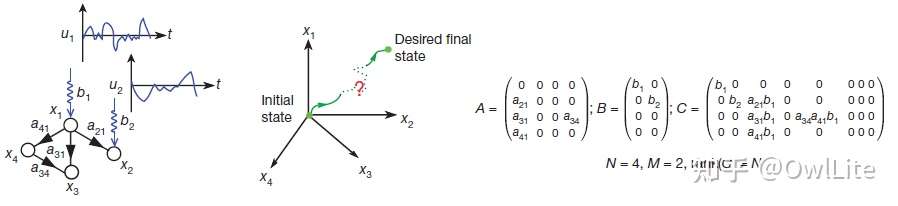
所以系统控制性问题转化为找到一个节点子集让 满秩的问题。但是实际情况中,我们很少能够确定性中各个节点之间的关系/影响力的权重
. 为了规避这个问题,我们可以将上面的定义的可控性问题转化为结构可控性问题,而不关心具体的权重[4]. 结构可控不涉及变量刻画,只关注逻辑关系,也就是不关注控制性的强弱。结构化系统
结构可控是指存在一组数值
使得
可控,也就是
满秩,这相当于寻找一个等价可控系统。
这个问题当然有暴力解法,但是存在一些基本的规律能帮助大幅缩小搜索空间,比如不包含输入或者输出节点的“最大匹配”(maximum matching)子网络:
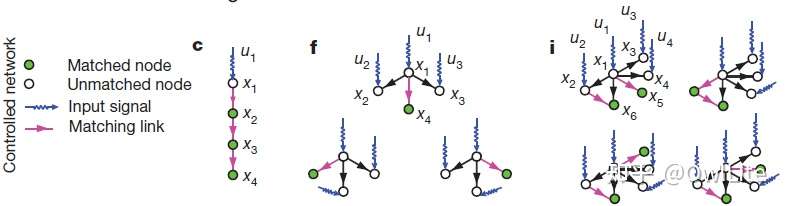
在实际系统中,我们可以用 描述系统的控制难度。
越小,系统的控制越容易。通过模拟发现,异质网络相比于同质网络具有更好的可控性。前者的典型包括社交网络(各人在社交网络中认识/被关注的人的数量分布差异巨大且稀疏性低)、组织(公司、工厂、政党等),后者的典型包括金融机构投资者、互联网、基因、脑网络(相对致密切同质)等。
进一步研究发现,被选出的控制子集中各个节点的度的分布比整个系统的度的分布取值显著偏低[5]. 这说明,想要控制整个系统,选取其中的Hub节点(关键节点,比如KOL,中层领导等)而忽略掉长尾节点进行控制并非明智做法。
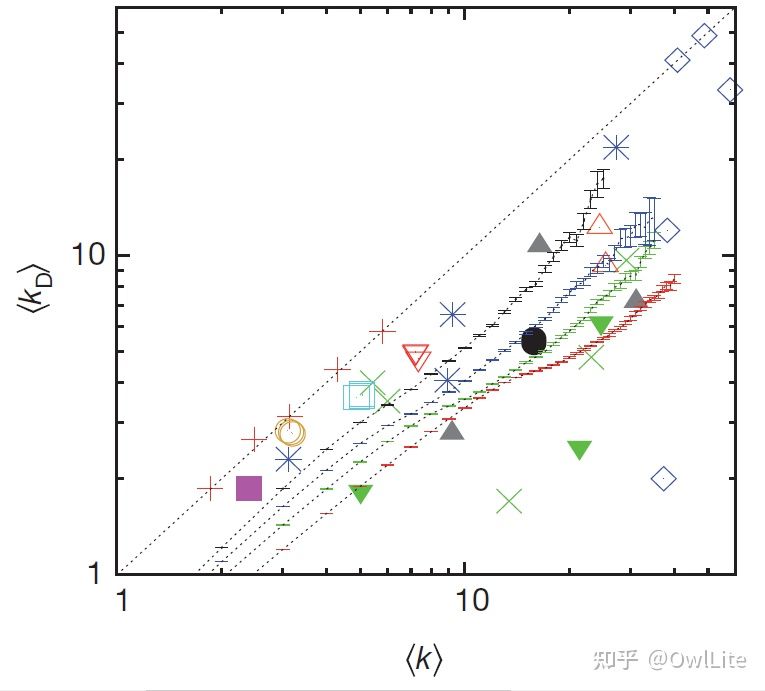
全系统的节点平均度K与控制字系统的节点平均度K_D
以上结果有些反直觉,但是跟现实具有很好的符合性[6]. 社交网络中的意见总是容易被营销等操作左右。从控制鲁棒性的角度来看,公司结构健康情况下具有很好的控制性和冗余性,也就是说“缺了谁公司都照样运转”。但是如果公司内部山头林立,领导不能听到基层意见,那么整个公司就走向了难以控制的状态,难以达成设计的业绩目标。在脑网络方面,由于大脑中每个子结构/系统都跟其他所有子结构/系统有直接或者间接的关系,该网络从控制角度来看是高度致密的,控制性低。所以我们在认知上总是观察到牵一发动全身的效果,精神性疾病往往叫做“综合症”而且很难根治。推荐系统的引入使得社区千人千面,也就是碎片化,分布同质化,导致社区的控制性和鲁棒性降低,进入高维护成本状态。
参考
^Liu, Y. Y., Slotine, J. J., & Barabási, A. L. (2011). Controllability of complex networks. nature, 473(7346), 167-173.
^Kalman, R. E. (1963). Mathematical description of linear dynamical systems. Journal of the Society for Industrial and Applied Mathematics, Series A: Control, 1(2), 152-192.
^Sontag, E. D. (1991). Kalman’s controllability rank condition: from linear to nonlinear. In Mathematical system theory (pp. 453-462). Springer, Berlin, Heidelberg.
^Lin, C. T. (1974). Structural controllability. IEEE Transactions on Automatic Control, 19(3), 201-208.
^Seidman, S. B. (1983). Network structure and minimum degree. Social networks, 5(3), 269-287.
^Cho, A. (2011). Scientific link-up yields ‘control panel’for networks.

